反向传播

简介

反向传播（英语：Backpropagation，缩写为BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。
反向传播要求有对每个输入值想得到的已知输出，来计算损失函数梯度。因此，它通常被认为是一种监督式学习方法，虽然它也用在一些无监督网络（如自动编码器）中。它是多层前馈网络的Delta规则的推广，可以用链式法则对每层迭代计算梯度。反向传播要求人工神经元（或“节点”）的激励函数可微。

梯度下降与损失函数

损失函数，(Loss Function）在机器学习中的每一种算法中都很重要，因为训练模型的过程就是优化损失函数的过程，损失函数对每个参数的偏导数就是梯度下降中提到的梯度，防止过拟合时添加的正则化项也是加在损失函数后面的。
损失函数非常好理解，我觉得其实就是，反映神经网络输出的结果与训练样本的y之间的差别的函数（其中输入变量是神经网络的权重参数）。这个函数要具有一些特性，一般情况下，我们要尽可能的最小化损失函数，寻找损失函数的全局最小值，

为了完成梯度下降

我们需要求偏导

过程

数学原理：基于复合函数求导的链式法则–
如果某个函数由复合函数表示，则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示；

简单线性回归

假设是 y=wx+b
其损失函数为

  • 随机初始化参数 w,b
  • 将w,b视为变量，x,y为常量
  • 根据梯度下降,更新w,b

、

因此需计算出、
易得= x , = 1
上面其实是现在的需求，根据链式法则

如下图，已知数据(1.5,0.8)，初始化参数w=0.8,b=0.2
一轮运算后得到预测值y=1.4
如果先得出,接着往下运算得到目标结果

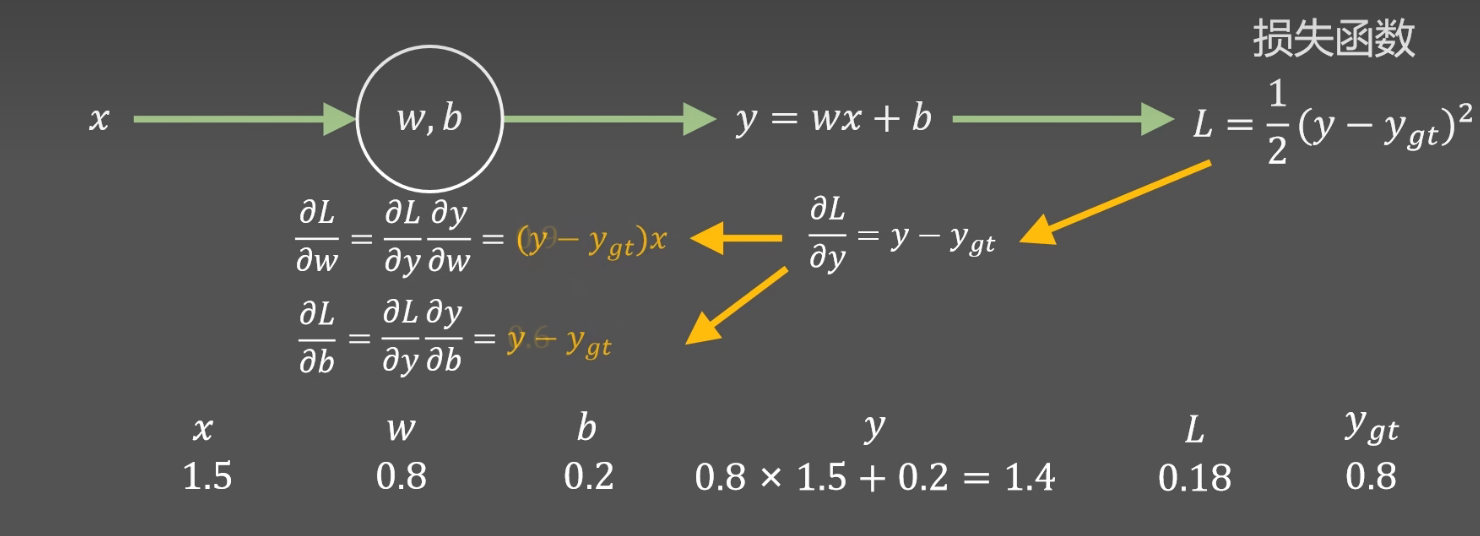
根据上图，= y - 其中为真实值，y是预测值，根据上面一轮的正向传播（即根据给定的模型计算得出），得到=1.4 -0.8 = 0.6

然后=0.6 x 1.5= 0.9 =0.6
然后设置学习率=0.1
更新w,b w=0.8-0.1 x 0.9 = 0.71 b=0.2-0.1 x 0.6=0.14
然后照此迭代模型
这样由后往前地求偏导就是反向传播的过程，

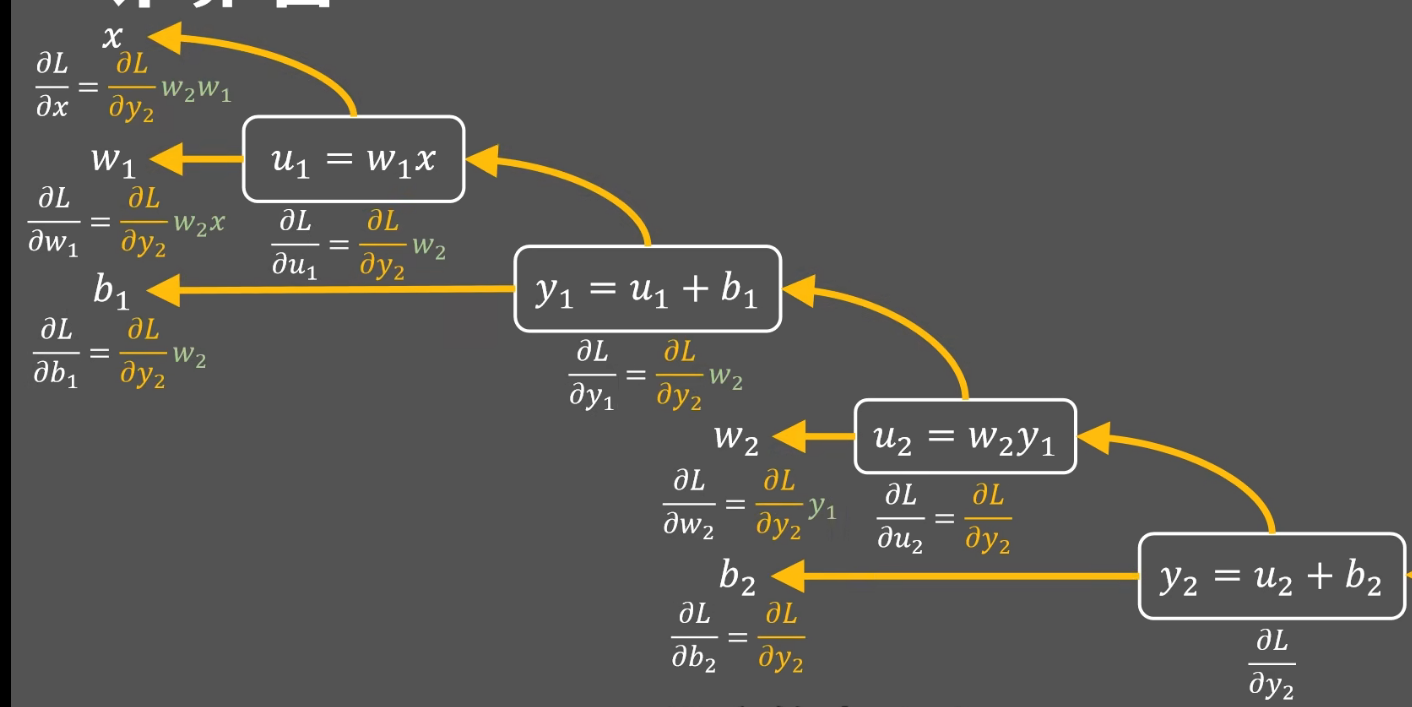
神经网络

在一个神经网络中，其实就是上面简单线性回归变得稍微复杂，多加上了几层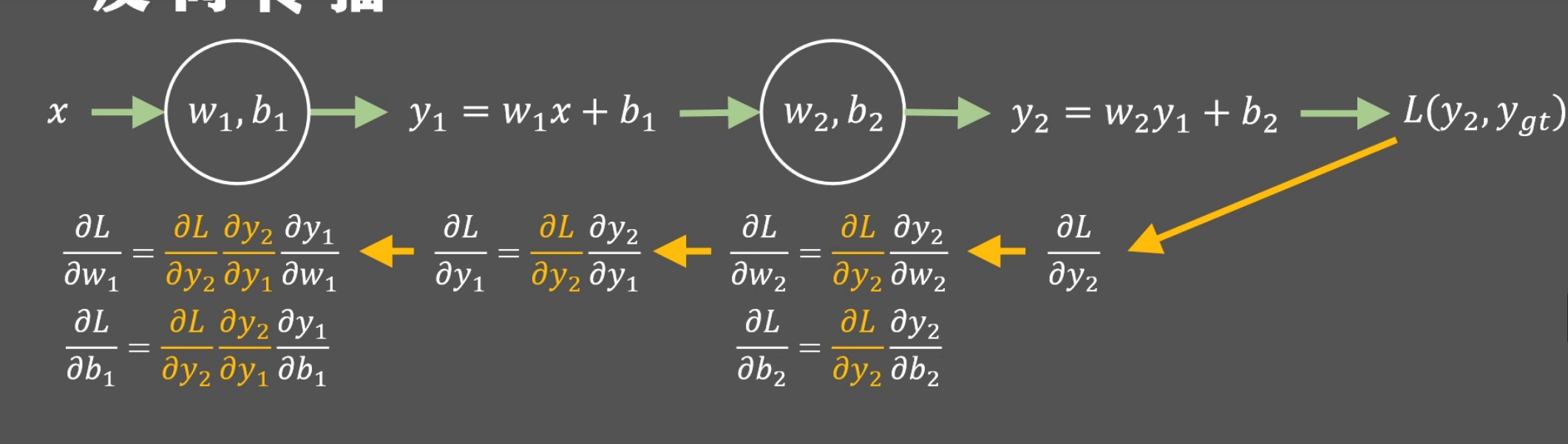

反向传播，根据上面一步的运算求出下一层次的偏导
就如上图，黄色部分其实都是已经由之前的运算得出
反向传播算法就是神经网络中加快计算梯度值的方法

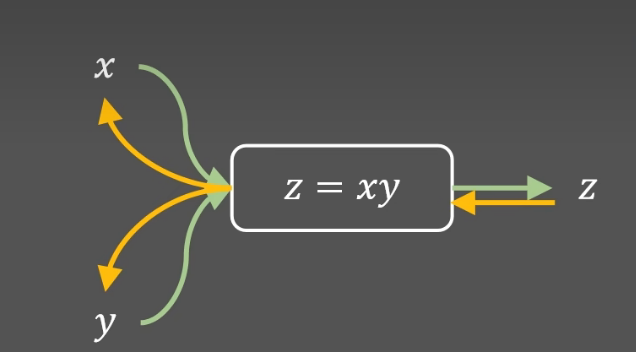
计算图

计算机中的运算并非就是上面图示的过程，因为很难对一个式子求偏导
，所以需要将式子拆开，由一个运算符连接得到计算图

计算图将计算过程用图形表示出来，这里的图形是指数据结构图，通过多个节点和边表示
用计算图解题时，需要按如下流程进行:

  • 构建计算图；
  • 在计算图上从左到右进行计算(正向传播, forward propagation)；
  • 在计算图上从右到左进行计算(反向传播, backward propagation)；
    • 将上游传过来的值E乘以节点的局部导数 ，然后将结果传递给下一个节点

计算图的优点:

  • 局部计算；
    • 无论全局多么复杂的计算，都可以通过局部计算使各个节点致力于简单的计算，从而简化问题；
  • 利用计算图可以将中间的计算结果保存起来；
  • 可以通过反向传播高效计算导数；
  • 综上:可以通过正向传播和反向传播高效地计算各个变量的导数值；

由计算图，可以定义每中运算的数据结构
如在Pytourch中乘法运算可以如下定义：

import torch.autograd

class Multiply(torch.autograd.Function):
    @staticmethod
    def forward(ctx,x,y):
        ctx.save_for_backward(x,y)
        z = x * y
        return z
    
    @staticmethod
    def backward(ctx,grad_z):
        x,y=ctx.save_tensors
        grad_x = grad_z * y
        grad_y = grad_z * x
        return grad_x,grad_y

forward函数是前向传播，计算 z =x * y
backward函数是反向传播 ，由参数grad_z （由上一级的梯度）计算对x,y的偏导
由于z= x*y
因此



backtop