线性回归（Linear Regression）

机器学习中的两大类问题：回归问题和分类问题

回归问题就是进行预测，如股票、房价预测
分类问题就是将多个事物进行分类

线性回归是一种用于预测连续数值输出的监督学习算法，它通过建立一个线性方程来描述输入变量与输出变量之间的关系。该算法的目标是使预测值与真实值之间的差异最小化。

概述

线性回归是通过一个或多个自变量与因变量之间进行建模的回归分析，其特点为一个或多个称为回归系数的模型参数的线性组合。样本点为历史数据，回归曲线要能最贴切的模拟样本点的趋势，将误差降到最小。

线性回归方程

线形回归方程，就是有 n 个特征，然后每个特征 **Xi **都有相应的系数 **Wi **，并且在所有特征值为0的情况下，目标值有一个默认值 **W0 **，因此：

整合后的公式为：

损失函数

公式

损失函数是一个贯穿整个机器学习的一个重要概念，大部分机器学习算法都有误差，我们需要通过显性的公式来描述这个误差，并将这个误差优化到最小值。
误差项：

用来表示真实值和预测值之间的差异

假设现在真实的值为 y，预测的值为 h ,损失函数为：

其实机器学习在算法大思想下，关键是如何迭代调整参数能使得误差变小，
一般情况下算法最后推出的数学公式也是无法直接计算求解

上面损失函数也就是所有误差和的平方。损失函数值越小，说明误差越小，这个损失函数也称最小二乘法。

公式推导

前提假设：误差是独立并具有相同的分布，并且服从均值为0，方差为的高斯分布

独立同分布（independent and identically distributed，i.i.d.）：
在概率统计理论中，指随机过程中，任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立，那么这些随机变量是独立同分布。

高斯分布：
即正态分布，概率密度函数如下如下：

这里就是取μ为0，即

将误差项计算公式,带入概率密度公式得到，预测准确的概率：

由于是多个样本，每个样本都是上面概率公式，这里就非常适合使用极大似然法，目标是求取一组W参数向量，使得概率取最大值
即求函数极值点
极大似然就不多说了，复习概率论就行

似然函数：

对似然函数取对数，将乘法转为加法

将上面得到式子化简得到：

求最大值转化为求下面的最小值

特殊解

目标函数：

化简：其中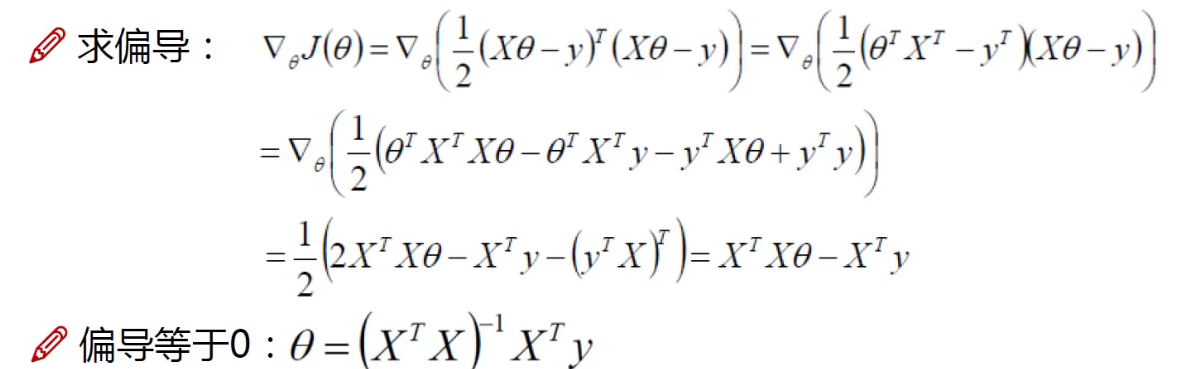

一般都不能直接算，因为这里只是特殊解，要求要有逆元

梯度下降


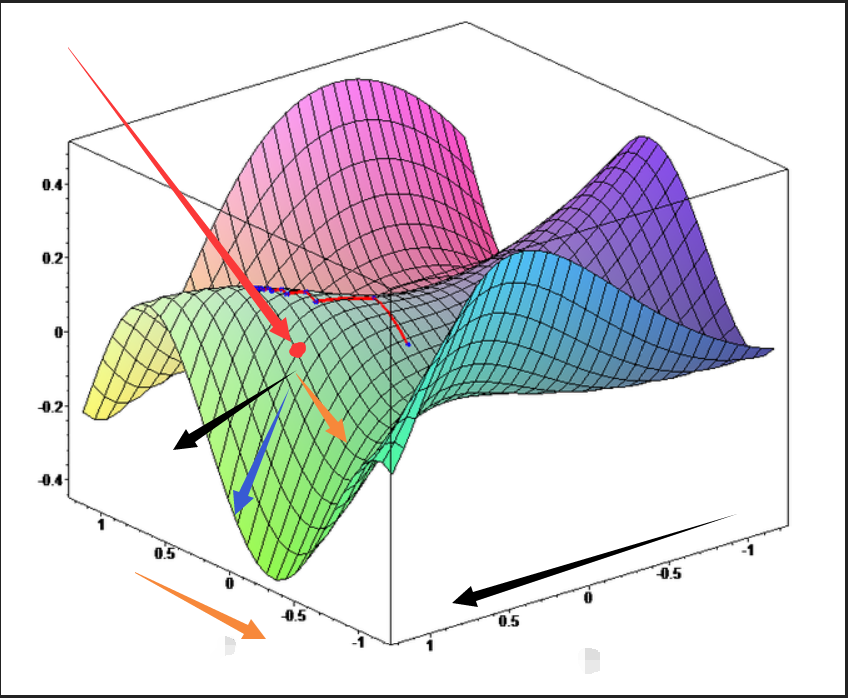
上面最小二乘法无法直接求解，但可以使用梯度下降算法逼近最小值

梯度就是函数对它的各个自变量求偏导后，由偏导数组成的一个向量。

数学推导：梯度下降法的数学原理 — 数据科学：从基础到实战 version 3a0c599
大概公式就是

λ表示步长或者说是学习系数，由我们定义，更加梯度下降原理，每次向着导数的反方向移动，就会逼近最小点

  • λ取太小，会陷入局部极值点
  • λ取太大，学习成本非常高

批量梯度下降（BGD）

批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新。
我们的目的是要误差函数尽可能的小，即求解weights使误差函数尽可能小。首先，我们随机初始化weigths，然后不断反复的更新weights使得误差函数减小，直到满足要求时停止。这里更新算法我们选择梯度下降算法，利用初始化的weights并且反复更新weights：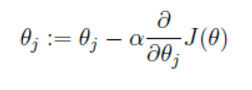

这里代表学习率，表示每次向着J最陡峭的方向迈步的大小。为了更新weights，我们需要求出函数J的偏导数。首先当我们只有一个数据点（x,y）的时候，J的偏导数是：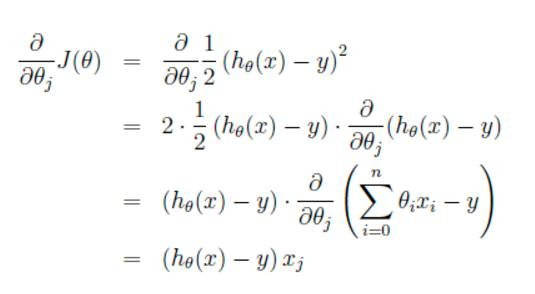

则对所有数据点，上述损失函数的偏导（累和）为：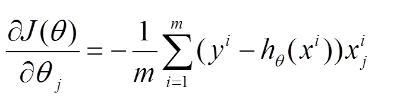

再最小化损失函数的过程中，需要不断反复的更新weights使得误差函数减小，更新过程如下：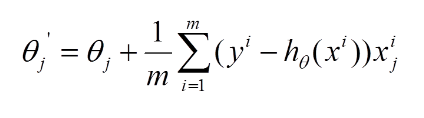

那么好了，每次参数更新的伪代码如下：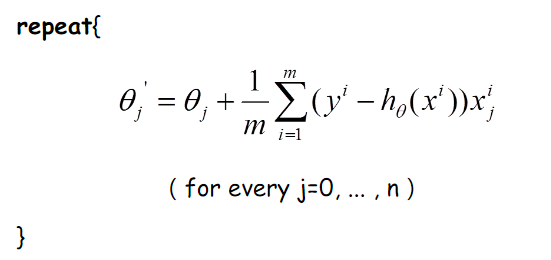

由上图更新公式我们就可以看到，我们每一次的参数更新都用到了所有的训练数据（比如有m个，就用到了m个），如果训练数据非常多的话，是非常耗时的。
下面给出批梯度下降的收敛图：


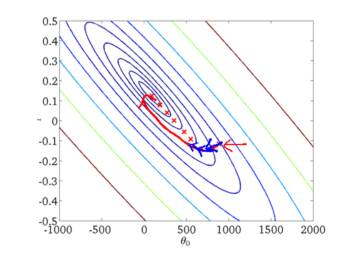
从图中，我们可以得到BGD迭代的次数相对较少。
代码实现：

def batchGradientDescent(x, y, theta, alpha, m, maxIteration):
    for i in range(maxIteration):
        hypothesis = np.dot(x, theta)
        loss = hypothesis - y
        gradient = np.dot(x.transpose(), loss) / m
        theta = theta - alpha * gradient              # 对所有样本求和
    return theta

随机梯度下降法（SGD）

由于批梯度下降每跟新一个参数的时候，要用到所有的样本数，所以训练速度会随着样本数量的增加而变得非常缓慢。随机梯度下降正是为了解决这个办法而提出的。它是利用每个样本的损失函数对θ求偏导得到对应的梯度，来更新θ：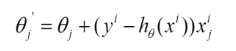

更新过程如下：

随机梯度下降是通过每个样本来迭代更新一次，对比上面的批量梯度下降，迭代一次需要用到所有训练样本（往往如今真实问题训练数据都是非常巨大），一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。
但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。
随机梯度下降收敛图如下：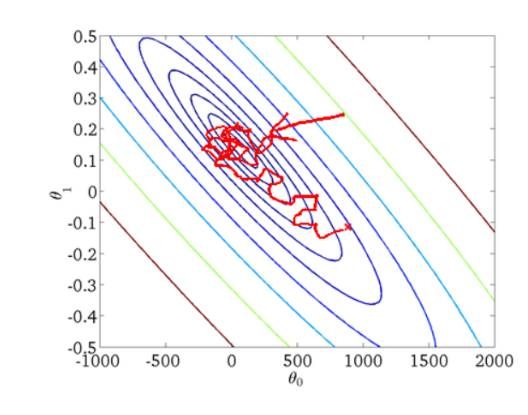

我们可以从图中看出SGD迭代的次数较多，在解空间的搜索过程看起来很盲目。但是大体上是往着最优值方向移动。
代码实现：

def StochasticGradientDescent(x, y, theta, alpha, m, maxIteration):
    data = []
    for i in range(10):
        data.append(i)
    # 这里随便挑选一个进行更新点进行即可（不用想BGD一样全部考虑）

    for i in range(maxIteration):
        hypothesis = np.dot(x, theta)
        loss = hypothesis - y  # 这里还是有十个样本
        index = random.sample(data, 1)[0]  # 随机抽取一个样本，得到它的下标
        gradient = loss[index] * x[index]  # 只取一个点进行更新计算
        theta = theta - alpha * gradient.T
    return theta

小批量梯度下降法（MBGD）

我们从上面两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？既算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）的初衷。
我们假设每次更新参数的时候用到的样本数为10个（不同的任务完全不同，这里举一个例子而已）
更新伪代码如下：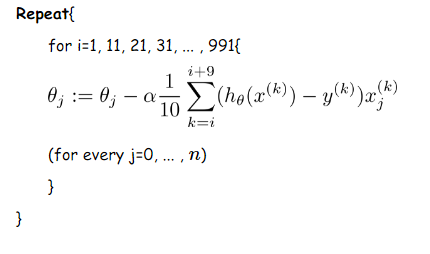

参考：

backtop